A operação de divisões é composta por dividendo, divisor, quociente e resto, no caso da divisão de polinômio por polinômio, considerando que cada um deles seja formado por mais de um monômio, iremos considerar a seguinte divisão:
P(x) |G(x)
R(x) D(x)
Onde P(x) é o dividendo; G(x) divisor; D(x) quociente e R(x) resto.
OBSERVAÇÃO: O resto em uma divisão de polinômio por polinômio pode ser:
• Igual à zero, nesse caso a divisão é exata, ou seja, o dividendo é divisível pelo divisor.
• Ou o resto pode ser diferente de zero, podendo assumir um valor real ou pode ser um polinômio, nesse caso será considerado resto um valor ou polinômio menor que o divisor.
A explicação de divisão de polinômio por polinômio será feita através de um exemplo, onde todos os passos tomados serão explicados.
Exemplo: resolva a seguinte divisão (6x4 – 10x3 + 9x2 + 9x – 5) : (2x2 – 4x + 5).
Antes de iniciarmos o processo da divisão é preciso fazer algumas verificações:
• Verificar se tanto o dividendo como o divisor está em ordem conforme as potências de x.
• Verificar se no dividendo, não está faltando nenhum termo, se estiver é preciso completar.
Feita as verificações podemos iniciar a divisão.
O dividendo possui 5 monômios (termos) e o divisor possui 3 monômios (termos).
6x4 – 10x3 + 9x2 + 9x – 5 | 2x2 – 4x + 5
• Iremos dividir o 1º termo do dividendo pelo primeiro termo do divisor:
6x4 : 2x2 = 3x2
• O resultado encontrado irá multiplicar o polinômio 2x2 – 4x + 5 (divisor).
(2x2 – 4x + 5) . (3x2) = 6x4 – 12x3 + 15x2
• O resultado desse produto deverá ser subtraído pelo polinômio 6x4 – 10x3 + 9x2 + 9x – 5 (dividendo).
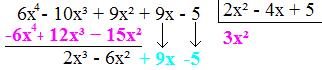
• Agora iremos levar em consideração o polinômio 2x3 – 6x2 + 9x - 5 e iremos dividir seu 1º termo pelo primeiro termo do dividendo (2x2 – 4x + 5).
2x3 : 2x2 = x
• O resultado encontrado irá multiplicar o polinômio 2x2 – 4x + 5 (divisor)
(2x2 – 4x + 5) . (x) = 2x3 – 4x2 + 5x
• O resultado desse produto deverá ser subtraído pelo polinômio 2x3 – 6x2 + 9x – 5.
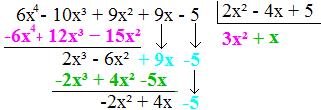
• Agora iremos levar em consideração o polinômio -2x2 +4x - 5e dividir seu 1º termo pelo primeiro termo do dividendo (2x2 – 4x + 5).
-2x2 : 2x2 = -1
• O resultado encontrado irá multiplicar o polinômio 2x2 – 4x + 5 (divisor)
(2x2 – 4x + 5) . (-1) = - 2x2 + 4x - 5
• O resultado desse produto deverá ser subtraído pelo polinômio -2x2 +4x – 5.
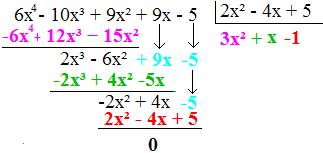
Portando, podemos dizer que (6x4 – 10x3 + 9x2 + 9x – 5) : (2x2 – 4x + 5) = 3x2 +x – 1, com resto igual a zero. Caso queira fazer a prova real, basta multiplicar (3x2 +x – 1) por 2x2 – 4x + 5 e verificar se a solução será 6x4 – 10x3 + 9x2 + 9x – 5. Nesse caso, como o resto é zero, não é preciso somá-lo ao produto.
P(x) |G(x)
R(x) D(x)
Onde P(x) é o dividendo; G(x) divisor; D(x) quociente e R(x) resto.
OBSERVAÇÃO: O resto em uma divisão de polinômio por polinômio pode ser:
• Igual à zero, nesse caso a divisão é exata, ou seja, o dividendo é divisível pelo divisor.
• Ou o resto pode ser diferente de zero, podendo assumir um valor real ou pode ser um polinômio, nesse caso será considerado resto um valor ou polinômio menor que o divisor.
A explicação de divisão de polinômio por polinômio será feita através de um exemplo, onde todos os passos tomados serão explicados.
Exemplo: resolva a seguinte divisão (6x4 – 10x3 + 9x2 + 9x – 5) : (2x2 – 4x + 5).
Antes de iniciarmos o processo da divisão é preciso fazer algumas verificações:
• Verificar se tanto o dividendo como o divisor está em ordem conforme as potências de x.
• Verificar se no dividendo, não está faltando nenhum termo, se estiver é preciso completar.
Feita as verificações podemos iniciar a divisão.
O dividendo possui 5 monômios (termos) e o divisor possui 3 monômios (termos).
6x4 – 10x3 + 9x2 + 9x – 5 | 2x2 – 4x + 5
• Iremos dividir o 1º termo do dividendo pelo primeiro termo do divisor:
6x4 : 2x2 = 3x2
• O resultado encontrado irá multiplicar o polinômio 2x2 – 4x + 5 (divisor).
(2x2 – 4x + 5) . (3x2) = 6x4 – 12x3 + 15x2
• O resultado desse produto deverá ser subtraído pelo polinômio 6x4 – 10x3 + 9x2 + 9x – 5 (dividendo).
• Agora iremos levar em consideração o polinômio 2x3 – 6x2 + 9x - 5 e iremos dividir seu 1º termo pelo primeiro termo do dividendo (2x2 – 4x + 5).
2x3 : 2x2 = x
• O resultado encontrado irá multiplicar o polinômio 2x2 – 4x + 5 (divisor)
(2x2 – 4x + 5) . (x) = 2x3 – 4x2 + 5x
• O resultado desse produto deverá ser subtraído pelo polinômio 2x3 – 6x2 + 9x – 5.
• Agora iremos levar em consideração o polinômio -2x2 +4x - 5e dividir seu 1º termo pelo primeiro termo do dividendo (2x2 – 4x + 5).
-2x2 : 2x2 = -1
• O resultado encontrado irá multiplicar o polinômio 2x2 – 4x + 5 (divisor)
(2x2 – 4x + 5) . (-1) = - 2x2 + 4x - 5
• O resultado desse produto deverá ser subtraído pelo polinômio -2x2 +4x – 5.
Portando, podemos dizer que (6x4 – 10x3 + 9x2 + 9x – 5) : (2x2 – 4x + 5) = 3x2 +x – 1, com resto igual a zero. Caso queira fazer a prova real, basta multiplicar (3x2 +x – 1) por 2x2 – 4x + 5 e verificar se a solução será 6x4 – 10x3 + 9x2 + 9x – 5. Nesse caso, como o resto é zero, não é preciso somá-lo ao produto.
Divisão de polinômios
Definição
Considere dois polinômios: A(x) denominado dividendo e B(x) denominado divisor, com B(x) ≠ 0.
Na divisão de A por B obtemos a função polinomial Q, denominada quociente, e a função polinomial R denominada resto, onde A(x) ≡ B(x) . Q(x) + R(x) e o grau do resto é menor que o grau do divisor.
Na divisão de A por B obtemos a função polinomial Q, denominada quociente, e a função polinomial R denominada resto, onde A(x) ≡ B(x) . Q(x) + R(x) e o grau do resto é menor que o grau do divisor.
Veja a representação:
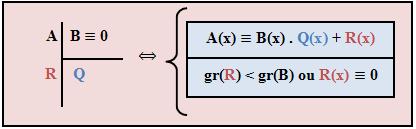
Veja no exemplo abaixo que se o grau do divisor for maior que o grau do dividendo, conseqüentemente o quociente será nulo e o resto será igual ao dividendo.
Exemplo:
Dividindo A(x) = x2 + 3x + 3 por B(x) x3 + 4x4 + 5 obtemos Q(x) = 0 e R(x) x2 + 3x + 3
Veja:
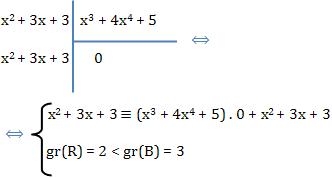
Agora veja um exemplo em que gr(A) ≥ gr(B):
Dividindo A(x) = x3 + 3x + 4 por B(x) = x2 – 1, obtemos Q(x) = x e R(x) = 4x + 4
Veja:
Veja:
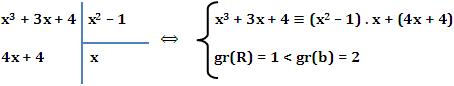
Cálculo de Q e R
A existência e a unicidade do quociente (Q) e do resto (R) da divisão de A por B, sendo B ≠ 0, é garantida. Ambos podem ser calculados através do Método da Chave.
Método da chave
Considerando os polinômios A e B já reduzidos e ordenados, podemos dizer que o Método da Chave é mecanismo prático que tem a função de obter o quociente (Q) e o resto (R), em diversas etapas, de uma forma semelhante a que fazemos na divisão euclidiana de números naturais.
Exemplo:
Na divisão A(x) = 2x3 + 7x2 + 4x – 4 por B(x) = x2 + 2x – 3 através do Método da Chave, temos:
1) Primeiro grupo de operações:
Dividimos o primeiro fragmento do dividendo pelo primeiro fragmento do divisor, obtendo assim a primeira parcela do quociente, e logo depois o primeiro resto parcial.
Lembre-se que: R = A – B . Q
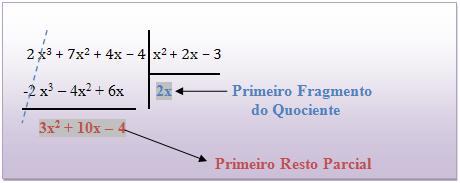
Conclusões:
►Como há o cancelamento do primeiro fragmento, o grau do dividendo é maior que o grau do resto parcial.
►2x3 + 7x2 + 4x – 4 ≡ (x2 + 2x – 3) . (2x) + (3x2 + 10 – 4)
►Como o grau do resto parcial não é menor que o grau do divisor, podemos dizer que a divisão ainda não foi concluída.
2) Segundo grupo de operações
Dividimos o primeiro fragmento do primeiro resto parcial pelo primeiro fragmento do divisor, obtendo assim o próximo fragmento do quociente, e logo depois o segundo resto parcial.
Lembre-se que: R = A – B . Q
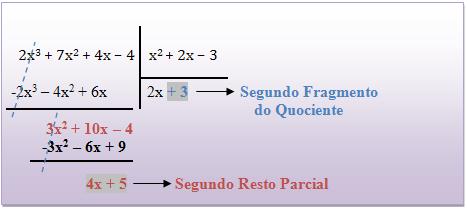
Conclusões:
►Como há o cancelamento do primeiro fragmento, o grau do primeiro resto parcial é maior do que o grau do segundo resto parcial.
►2x3 + 7x2 + 4x – 4 ≡ (x2 + 2x – 3) . (2x + 3) + (4x + 5)
►Como o grau do divisor é maior do que o grau do segundo resto parcial, podemos dizer que a divisão foi concluída.
Portanto:
Da divisão 2x3 + 7x2 + 4x – 4 por x2 + 2x – 3 obtemos:
Q(x) = 2x + 3
R(x) = 4x + 5
Método de Descartes
É um método também conhecido como Método dos Coeficientes a Determinar, que tem como funções
– formar o quociente Q, em função de coeficientes a serem determinados, sendo que gr(Q) = gr(A) – gr(B).
– formar o resto R, em função de coeficientes a serem determinados, sendo que gr(R) < gr(B) ou R(x) ≡ 0.
– aproveitar a definição da divisão.
– através da identificação dos polinômios, obter os coeficientes Q e R.


Nenhum comentário:
Postar um comentário